Newest Post
RESEÑA HISTORICA
La definición de matrices aparece por primera vez en
el año 18501, introducida por J.J Sylvester. Sin embargo hace más de dos mil
años los matemáticos chinos habían descubierto ya un método de resolución de
sistemas de ecuaciones lineales y por lo tanto, empleaban tablas con números.
El desarrollo inicial de la teoría de matrices se debe
al matemático W.R Hamilton en 1853. En 185¡8 Arthur Cayley introduce la notación
matricial como una forma abreviada de escribir un sistema de m ecuaciones
lineales con n incógnitas, la misma que fue descrita en su publicación
"memorias sobre la teoría de matrices".
En esta publicación, Cayley daba la definición de
matriz y las operaciones de suma entre matrices, de la multiplicación de un número
real por una matriz de la multiplicación entre matrices y de la inversa de una
matriz.
Las matrices de utilizan en el cálculo numérico den la
resolución de sistemas de ecuaciones lineales que surgen de problemas redes de producción,
en la resolución de las ecuaciones diferenciales y las derivadas parciales
temas que se analizaran en cursos superiores de cálculo.
La utilización de matrices constituye actualmente una
parte esencial de los lenguajes de programación ya que la mayoría de datos se
introducen en las computadoras como tablas organizadas en filas y columnas:
hojas de cálculo, base de datos, entre otros.
Definición
Una matriz es un arreglo bidimensional de números
(llamados entradas de la matriz) ordenados en filas (o renglones)
y columnas, donde una fila es cada una de las líneas horizontales
de la matriz y una columna es cada una de las líneas verticales. A una matriz
con n filas y m columnas se le denomina
matriz n-por-m (escrito )
donde
)
donde 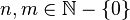 .
El conjunto de las matrices de tamaño
.
El conjunto de las matrices de tamaño  se
representa como
se
representa como  ,
donde
,
donde  es
el campo al cual pertenecen las
entradas. El tamaño de una matriz siempre se da con el número de filas primero
y el número de columnas después.
es
el campo al cual pertenecen las
entradas. El tamaño de una matriz siempre se da con el número de filas primero
y el número de columnas después.
 )
donde
)
donde 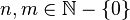 .
El conjunto de las matrices de tamaño
.
El conjunto de las matrices de tamaño  se
representa como
se
representa como  ,
donde
,
donde  es
el campo al cual pertenecen las
entradas. El tamaño de una matriz siempre se da con el número de filas primero
y el número de columnas después.
es
el campo al cual pertenecen las
entradas. El tamaño de una matriz siempre se da con el número de filas primero
y el número de columnas después.
Dos matrices se dice que son iguales si tienen el mismo tamaño y los mismos
elementos en las mismas posiciones.
A la entrada de una matriz que se encuentra en la fila 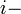 ésima y
la columna
ésima y
la columna 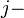 ésima se
le llama entrada
ésima se
le llama entrada  o
entrada
o
entrada 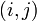 -ésimo
de la matriz. En estas expresiones también se consideran primero las filas y
después las columnas.
-ésimo
de la matriz. En estas expresiones también se consideran primero las filas y
después las columnas.
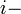 ésima y
la columna
ésima y
la columna 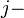 ésima se
le llama entrada
ésima se
le llama entrada  o
entrada
o
entrada 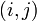 -ésimo
de la matriz. En estas expresiones también se consideran primero las filas y
después las columnas.
-ésimo
de la matriz. En estas expresiones también se consideran primero las filas y
después las columnas.
Se denota a las matrices con letra mayúscula, mientras que se utiliza la
correspondiente letra en minúsculas para denotar a las entradas de las mismas,
con subíndices que refieren al número de fila y columna del elemento.4 Por
ejemplo, al elemento de una matriz  de
tamaño
de
tamaño  que
se encuentra en la fila
que
se encuentra en la fila 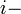 ésima y
la columna
ésima y
la columna 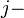 ésima se
le denota como
ésima se
le denota como 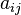 ,
donde
,
donde 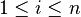 y
y 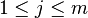 .
.
 de
tamaño
de
tamaño  que
se encuentra en la fila
que
se encuentra en la fila 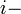 ésima y
la columna
ésima y
la columna 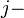 ésima se
le denota como
ésima se
le denota como 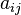 ,
donde
,
donde 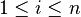 y
y 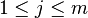 .
.
Cuando se va a representar explícitamente una entrada la cuál está indexada
con un 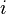 o un
o un  con
dos cifras se introduce una coma entre el índice de filas y de columnas. Así
por ejemplo, la entrada que está en la primera fila y la segunda columna de la
matriz
con
dos cifras se introduce una coma entre el índice de filas y de columnas. Así
por ejemplo, la entrada que está en la primera fila y la segunda columna de la
matriz  de
tamaño
de
tamaño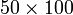 se
representa como
se
representa como 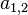 mientras
que la entrada que está en la fila número 23 y la columna 100 se representa
como
mientras
que la entrada que está en la fila número 23 y la columna 100 se representa
como 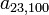 .
.
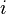 o un
o un  con
dos cifras se introduce una coma entre el índice de filas y de columnas. Así
por ejemplo, la entrada que está en la primera fila y la segunda columna de la
matriz
con
dos cifras se introduce una coma entre el índice de filas y de columnas. Así
por ejemplo, la entrada que está en la primera fila y la segunda columna de la
matriz  de
tamaño
de
tamaño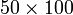 se
representa como
se
representa como 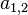 mientras
que la entrada que está en la fila número 23 y la columna 100 se representa
como
mientras
que la entrada que está en la fila número 23 y la columna 100 se representa
como 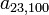 .
.
Además de utilizar letras mayúsculas para representar matrices, numerosos
autores representan a las matrices con fuentes en negrita para distinguirlas de
otros objetos matemáticos. Así  es
una matriz, mientras que
es
una matriz, mientras que  es
un escalar en esa notación. Sin embargo
ésta notación generalmente se deja para libros y publicaciones, donde es
posible hacer ésta distinción tipográfica con facilidad. En otras notaciones se
considera que el contexto es lo suficientemente claro como para no usar
negritas.
es
un escalar en esa notación. Sin embargo
ésta notación generalmente se deja para libros y publicaciones, donde es
posible hacer ésta distinción tipográfica con facilidad. En otras notaciones se
considera que el contexto es lo suficientemente claro como para no usar
negritas.
 es
una matriz, mientras que
es
una matriz, mientras que  es
un escalar en esa notación. Sin embargo
ésta notación generalmente se deja para libros y publicaciones, donde es
posible hacer ésta distinción tipográfica con facilidad. En otras notaciones se
considera que el contexto es lo suficientemente claro como para no usar
negritas.
es
un escalar en esa notación. Sin embargo
ésta notación generalmente se deja para libros y publicaciones, donde es
posible hacer ésta distinción tipográfica con facilidad. En otras notaciones se
considera que el contexto es lo suficientemente claro como para no usar
negritas.
Otra notación, en sí un abuso de notación, representa a la matriz por sus
entradas, i.e. 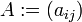 o
incluso
o
incluso 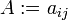 .
.
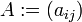 o
incluso
o
incluso 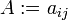 .
.
Como caso particular de matriz, se definen los vectores fila y los vectores
columna. Un vector fila o vector renglón es
cualquier matriz de tamaño  mientras
que un vector columna es cualquier matriz de
tamaño
mientras
que un vector columna es cualquier matriz de
tamaño 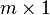 .
.
 mientras
que un vector columna es cualquier matriz de
tamaño
mientras
que un vector columna es cualquier matriz de
tamaño 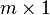 .
.
A las matrices que tienen el mismo número de filas que de columnas, 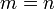 , se les
llama matrices cuadradas y el conjunto se
denota
, se les
llama matrices cuadradas y el conjunto se
denota 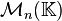 ,
alternativamente a la notación usual
,
alternativamente a la notación usual  .
.
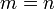 , se les
llama matrices cuadradas y el conjunto se
denota
, se les
llama matrices cuadradas y el conjunto se
denota 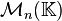 ,
alternativamente a la notación usual
,
alternativamente a la notación usual  .
.
Ejemplo
Dada la matriz 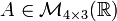
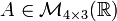
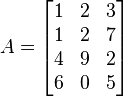
es una matriz de tamaño  . La
entrada
. La
entrada  es
7.
es
7.
 . La
entrada
. La
entrada  es
7.
es
7.
La matriz 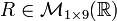
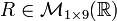
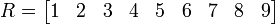
es una matriz de tamaño 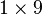 : un
vector fila con 9 entradas.
: un
vector fila con 9 entradas.
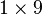 : un
vector fila con 9 entradas.
: un
vector fila con 9 entradas.
Clasificación de las
Matrices
La matriz es un concepto principal, no sólo en el campo de las matemáticas,
sino en el de las Computadoras también. Una matriz puede definirse simplemente
como una ordenación rectangular de números reales o complejos. Cada número o entrada
en una matriz es llamado un elemento de la matriz. Los elementos incluidos en
la línea horizontal forman una fila de la matriz. Los elementos incluidos en la
línea vertical forman una columna de la matriz. Una matriz es de diversos tipos
y formas. Se pueden clasificar en:
1). Matriz columna 2). Matriz fila 3). Matriz cuadrada 4). Matriz diagonal
5). Matriz identidad o unidad 6). Matriz cero o nula 7). Matriz simétrica 8).
Matriz asimétrica
Entremos en los detalles de cada una:
1). Matriz columna: Una matriz con n filas y 1 columna, se denomina matriz
columna. Esta matriz es de tipo m x 1.
Por ejemplo: 
2). Matriz fila: Una matriz que tiene una fila y n columnas, se dice que es
una matriz fila. Esta matriz es del tipo 1 x n.
Por ejemplo: 
3). Matriz Cuadrada: Una matriz en la cual el número de columnas es igual
al número de filas, se conoce como una matriz cuadrada. Una matriz de orden n
es aquella que tiene n filas y n columnas. La propiedad aceptada en la matriz
cuadrada es que dos o más matrices cuadradas de orden idéntico, pueden
multiplicarse, sumarse y restarse.
Por ejemplo: 
4). Matriz diagonal: En una matriz cuadrada, los elementos para los cuales
i = j, se denominan elementos diagonales. Una matriz cuadrada donde cada
elemento, excepto los elementos diagonales, son iguales a cero, es llamada
matriz diagonal. La matriz diagonal se denomina a veces matriz diagonal
rectangular.
Por ejemplo: 
5). Matriz identidad o unidad: Se dice que una matriz es la matriz
identidad o unidad, si cada elemento de la diagonal principal de la matriz
particular es 1. La matriz identidad generalmente es denotada por ‘I’. Este
tipo de matriz tiene la siguiente propiedad:
AI = A y IA = A
Por ejemplo: 
6). Matriz cero o nula: Se trata de una matriz en la cual cada elemento es
igual a 0. Se representa como ‘0’. Si ‘O’ es la matriz cero m × n y A es
cualquier matriz m × n, entonces A + O = O A. En consecuencia O es la identidad
aditiva de la suma de matrices.
Por ejemplo: 
7). Matriz simétrica: Una matriz simétrica se refiere a la matriz cuadrada
cuyo valor es igual al transpuesto de la matriz. Es decir, .La simetría de la
diagonal simétrica está relacionada con la diagonal principal. Por otra parte,
toda matriz diagonal es simétrica.
Por ejemplo: 
8). Matriz asimétrica: La matriz asimétrica también es conocida como matriz
antimétrica o antisimétrica. Se trata de una matriz cuyo valor de transposición
es negativo de su valor. Es decir,
A = -AT.
Estos ocho tipos son la base de la clasificación de las matrices. Estos
pueden utilizarse para generar una clasificación más precisa. Sin embargo, el
concepto básico y el método de operación en las matrices son idénticos en todas
las clasificaciones.
Propiedades entre matrices
Sean 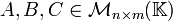 ,
donde
,
donde  es
un campo entonces se cumplen las siguientes propiedades para la operación
binaria.
es
un campo entonces se cumplen las siguientes propiedades para la operación
binaria.
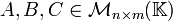 ,
donde
,
donde  es
un campo entonces se cumplen las siguientes propiedades para la operación
binaria.
es
un campo entonces se cumplen las siguientes propiedades para la operación
binaria.
Asociatividad
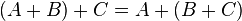
Conmutatividad
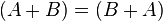
Existencia del elemento neutro aditivo
Existe 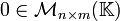 tal que
tal que
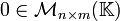 tal que
tal que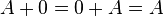
Existencia del inverso aditivo
Existe
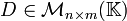 tal que
tal que
a esta matriz  se le denota por
se le denota por 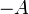
 se le denota por
se le denota por 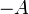
OPERACIONES CON MATRICES
Suma de matrices
Dadas dos matrices de la misma
dimensión, A=(aij) y B=(bij), se define la matriz suma
como: A+B=(aij+bij). Es decir, aquella matriz cuyos
elementos se obtienen: sumando los elementos de las dos matrices que ocupan la
misma misma posición.
Propiedades
- Interna:
- Asociativa: A + (B + C) = (A + B) + C
- Elemento neutro: A + 0 =
A
- Elemento opuesto:A +
(−A) = O
- Conmutativa: A + B = B + A
Producto de un número real por una
matriz
Dada una matriz A=(aij)
y un número real k R, se
define el producto de un número real por una matriz: a la matriz del mismo
orden que A, en la que cada elemento está multiplicado por k.
R, se
define el producto de un número real por una matriz: a la matriz del mismo
orden que A, en la que cada elemento está multiplicado por k.
kA=(k aij)
Propiedades
- a · (b · A) = (a · b) · A A
Mmxn, a, b
- a · (A+B) = a · A + a · B A,B
Mmxn , a
- (a+b) · A = a · A+b · A A
Mmxn , a, b
- 1 · A = A A
Mmxn
Producto de matrices
Dos matrices A y B se dicen multiplicables si el número de columnas de A coincide
con el número de filas de B.
Mm
x n x Mn x p = M m x p
El elemento cij de la matriz producto se obtiene
multiplicando cada elemento de la fila i de la matriz A por cada elemento de la
columna j de la matriz B y sumándolos.
DETERMINANTES
A =
Determinante de orden uno
|a 11| = a 11
Determinante de orden dos
 = a 11 a 22 - a 12 a 21
= a 11 a 22 - a 12 a 21

Determinante de orden tres
Consideremos una matriz 3 x 3 arbitraria A = (aij).
El determinante de A se define como sigue: =
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 -
=
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 -
 =
3 · 2 · 4 + 2 · (-5) · (-2) + 1 · 0 ·
1 -
=
3 · 2 · 4 + 2 · (-5) · (-2) + 1 · 0 ·
1 -
MÉTODO PARA ENCONTRAR EL DETERMINANTE DE UNA MATRIZ
Con la tecnología de Blogger.