FUNCIONES

Newest Post

FUNCIONES

// Posted by :Unknown // On :domingo, 19 de julio de 2015

RESEÑA HISTORICA

Según García (2001) el término función fue utilizado por primera vez en 1637 por el matemático y filosofo francés René Descartes (1596-1650), él mostró en sus trabajos de geometría que tenía una idea muy clara de los conceptos de ``variable'' y ``función'', realizando una clasificación de las curvas algebraicas según sus grados, reconociendo que los puntos de intersección de dos curvas se obtienen resolviendo, en forma simultanea, las ecuaciones que las representan, Descartes lo uso por primera vez para designar una potencia xn de la variable x.

“En 1694 el matemático alemán Gottfried Wilhelm Leibniz utilizó el término para referirse a varios aspectos de una curva, como su pendiente”.

En la obra Introduction in Analysis Infinitorum, Leonhard Euler intenta por primera vez dar una definición formal del concepto de función al afirmar que: "Una función de cantidad variable es una expresión analítica formada de cualquier manera por esa cantidad variable y por números o cantidades constantes''. como puede observarse, esta definición difiere de la que actualmente se conoce, pues siete años después, en el prólogo de las Instituciones, calculo diferencial, afirmó:''Algunas cantidades en verdad dependen de otras, si al ser combinadas las ultimas las primeras también sufren cambio, y entonces las primeras se llaman funciones de las últimas. Esta denominación es bastante natural y comprende cada método mediante el cual una cantidad puede ser determinada por otras. Así, si x denota una cantidad variable, entonces todas las cantidades que dependen de x en cualquier forma están determinadas por x y se les llama funciones de x''.

“En la historia de las matemáticas se le dan créditos al matemático suizo Leonhard Euler (1707-1783) por precisar el concepto de función, así como por realizar un estudio sistemático de todas las funciones elementales, incluyendo sus derivadas e integrales; sin embargo, el concepto mismo de función nació con las primeras relaciones observadas entre dos variables, hecho que seguramente surgió desde los inicios de la matemática en la humanidad, con civilizaciones como la babilónica, la egipcia y la china”.

Según García (2001), hasta recientemente, su uso más generalizado ha sido el definido en 1829 por el matemático alemán Peter Dirichlet. Dirichlet entendió la función como una variable y, llamada variable dependiente, cuyos valores son fijados o determinados de una forma definida según los valores que se asignen a la variable independiente x, o a varias variables independientes x1, x2, ..., xk.

“Los valores, tanto de la variable dependiente, como de las variables independientes, son números reales o complejos. La expresión y = f(x), leída “y es función de x” indica la interdependencia entre las variables x e y; f(x) se daba normalmente en forma explícita, como f(x) = x2 - 3x + 5, o mediante una regla expresada en palabras, como f(x) es el primer entero mayor que x para todos aquellos x que sean reales. Si a es un número, entonces f(a) es el valor de la función para el valor x = a. Así, en el primer ejemplo, f(3) = 32 - 3 • 3 + 5 = 5, f(-4) = (-4)2 - 3(-4) + 5 = 33; en el segundo ejemplo, f(3) = f(3,1) = f(p) = 4”.

La aparición de la teoría de conjuntos primero extendió, y luego alteró sustancialmente, el concepto de función. El concepto de función en las matemáticas de nuestros días queda ilustrado a continuación. Sean X y Y dos conjuntos con elementos cualquiera; la variable x representa un elemento del conjunto X, y la variable Y representa un elemento del conjunto Y. Los elementos de ambos conjuntos pueden ser o no números, y los elementos de X no tienen que ser necesariamente del mismo tipo que los de Y.

El concepto moderno de función está relacionado con la idea de Dirichlet. Dirichlet consideró que y = x2 - 3x + 5 era una función; hoy en día, se considera que y = x2 - 3x + 5 es la relación que determina la y correspondiente a una x dada para un par ordenado de la función ; así, la relación anterior determina que (3, 5), (-4, 33) son dos de los infinitos elementos de la función. Aunque y = f(x) se usa hoy todavía, es más correcto si se lee “y está funcionalmente relacionado con x”.

Las funciones se denominan también transformaciones o aplicaciones en muchas ramas de las matemáticas. Si el conjunto Y1 es un subconjunto propio de Y (esto es, al menos una y pertenece a Y pero no a Y1), entonces F es una función, transformación o aplicación del dominio X1 en Y; si Y1 = Y, F es una función, transformación o aplicación de X1 sobre Y.

RELACIONES Y FUNCIONES

Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamado Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Rango.

Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.

podemos deducir que todas las funciones son relaciones, pero no todas las relaciones son funciones. También debemos agregar que toda ecuación es una Relación, pero no toda ecuación es una Función. Todas las Relaciones pueden ser graficadas en el Plano Cartesiano.

PAR ORDENADO

Es un conjunto de 2 elementos a y b, que tienen un orden. Al elemento a se lo denomina primera componente y, al elemento b se lo denomina segunda componente. se lo representa de la siguiente manera:

(a,b) par ordenado

PLANO CARTESIANO

Sean a y b conjuntos no vacíos vamos a dominar producto cartesiano entre a y b, al conjunto de todos los pares osdenados cuya primera componente pertenece al conjunto a, y la segunbda componente pertenecen al grupo b, su representación es:
AxB= {Cx,y) / x € A) ^ (y € b)}

x € A (x,y) € A x B
y € B

Resultado de imagen para plano cartesiano

A = { ☺, ☻, ♥}

B = {♦,♣}

AxB = {(☺,♦), (☺,♣),(☻,♦),(☻,♣),(♥,♦),(♥,♣)}

N(A) = 3

N(B) = 2

N(AXB) = (N(A) N(B))

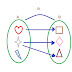
DOMINIO DE UNA RELACION

El dominio de una relación son todos los conjuntos del elemento de partida que tiene relación con el conjunto de llegada, su representación simbólica es: DomR

RANGO

Conocido también como co-dominio. Son todos los elementos del conjunto de llegada que tienen relación con el dominio del conjunto de partida. Su representación simbólica es:

rg R.

DomR = {♥,☆}

Rg R = {□,◊,Δ}

TIPOS DE FUNCIONES

INYECTIVA.

F Es una función inyectiva si a cada elemento del rango es imagen exclusiva de un único elemento del dominio, además es necessario que N(A) ≤ N(B).

A = {2,4,6,8}

B = {2,5,7,9,10}

SOBREYECTIVA.

F es una función sobreyectiva si el rango es B, además es necesario que N(A) ≥ N(B)

A = { 6,8,10,12,14}
B = { 1,2,3,4}

FUNCIÓN REAL DE VARIABLE REAL

Se llama función real de variable real a toda función definida de un subconjunto D de los números reales, en el conjunto R de los números reales, tal que a cada elementox de D le corresponde uno y sólo un elemento y de R:

Para que una función quede correctamente definida es necesario determinar:

· El conjunto inicial o dominio de la función.

· El conjunto final o imagen de la función.

· La regla por la cual se asigna a cada elemento del conjunto origen un solo elemento del conjunto imagen.

Así, por ejemplo, la función definida por:

asigna a cada número real su cuadrado.

Tiene por conjunto origen o campo de existencia todos los números reales, pues dado cualquier número real x, siempre es posible calcular su cuadrado, siendo el resultado otro número real.

Tiene por conjunto imagen todos los números reales positivos, puesto que el cuadrado de un número siempre es positivo:

La regla de asignación es «dado cualquier número real x, calcular su cuadrado para obtener la imagen».

Ejemplo:

Hallar el campo de existencia de la función f definida por

Resolución:

· La función anterior asigna a cada número x, el valor

El campo de existencia está formado por todos los números reales x, para los que su imagen está definida mediante la función f.

aquellos que anulen el denominador, puesto que la expresión 1/0 no es un número real. El denominador x - 2 se anula cuando x = 2.

Por tanto, el campo de existencia de la función es R - {2}.

Su representación mediante intervalos es C.E. = (-¥, 2) È (2, +¥)

Resolución:

cero, puesto que las raíces cuadradas de los números negativos no tienen sentido en el conjunto de los números reales.

Luego C.E. = (-¥, -3] È [3, +¥).

· Por tanto, al campo de existencia pertenecen todos los números reales excepto el 3 y el -2.

-3, 0, 3 y 5. ¿Cuál es su dominio de definición? ¿Hay algún número que se transforme en el 0?

Resolución:

· Campo de existencia:

El denominador nunca se hace cero, ya que x² + 2 > 0 para cualquier x. Si

de existencia de esta función es toda la recta real R.

· Para responder a la pregunta siguiente, hay que estudiar si existe algún número x, tal que f(x) = 0.

TIPOS DE FUNCIONES

1. Funciones algebraicas

En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.

Las funciones algebraicas pueden ser:

Funciones explícitas

Si se pueden obtener las imágenes de x por simple sustitución.

f(x) = 5x − 2

Funciones implícitas

Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.

5x − y − 2 = 0

1.1 Funciones polinómicas

Son las funciones que vienen definidas por un polinomio.

f(x) = a₀+ a₁x + a₂x² + a₂x³ +··· + a_nxⁿ

Su dominio es

, es decir, cualquier número real tiene imagen.

1.1.1 Funciones constantes

El criterio viene dado por un número real.

f(x)= k

La gráfica es una recta horizontal paralela a al eje de abscisas.

1.1.2 Funciones polinómica de primer grado

f(x) = mx + n

Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.

Son funciones de este tipo las siguientes:

Función afín.

Función lineal.

Función identidad.

1.1.3 Funciones cuadráticas

f(x) = ax² + bx + c

Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.

1.2 Funciones racionales

El criterio viene dado por un cociente entre polinomios:

El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.

1.3 Funciones radicales

El criterio viene dado por la variable x bajo el signo radical.

El dominio de una función irracional de índice impar es R.

El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.

1.4 Funciones algebraicas a trozos

Son funciones definidas por distintos criterios, según los intervalos que se consideren.

Funciones en valor absoluto.

Función parte entera de x.

Función mantisa.

Función signo.

2. Funciones trascendentes

La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.

2.1 Funciones exponenciales

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia a^xse llama función exponencial de base a y exponente x.

2.2 Funciones logarítmicas

La función logarítmica en base a es la función inversa de la exponencial en base a.

2.3 Funciones trigonométricas

Función seno

f(x) = sen x

Función coseno

f(x) = cos x

Función tangente

f(x) = tg x

Función cosecante

f(x) = cosec x

Función secante

f(x) = sec x

Función cotangente

f(x) = cotg x

Técnicas de Graficación

Desplazamiento vertical de las graficas

y = f(x) + k ( k > 0)

y = f(x) - k ( k > 0)

Observa que la gráfica de y = x² + 2 sube dos unidades desde el origen y la gráfica de y = x² - 3 baja tres unidades desde el origen.

Nota: La gráfica de la ecuación de la forma y = f(x) + k es la gráfica de y = f(x) desplazada hacia arriba si k es positiva y desplazada hacia abajo si k es negativa. De manera que, la gráfica de y = f(x) + k se puede obtener de la gráfica de y = f(x) al trasladar verticalmente la gráfica de y = f(x), k unidades hacia arriba si k es positiva y k unidades hacia abajo si k es negativa.

Desplazamiento Horizontal de las Graficas

y = f(x - h) ( k > 0)

y = f(x + h) ( k > 0)

Observa que la gráfica de y = ( x + 2)² se mueve dos unidades hacia la izquieda y la gráfica de y = (x - 2)² se mueve dos unidades hacia la derecha.

Nota: La gráfica de y = f(x + h) es la gráfica de y = f(x) desplazada hacia la derecha si h es negativa y desplazada hacia la izquierda si h es positiva. De manera que, la gráfica de y = f( x + h) se puede obtener de la gráfica de y = f(x) al trasladar horizontalmente la gráfica de y = f(x), h unidades hacia la izquierda si h es positiva y h unidades hacia la derecha si h es negativa.

Ejemplo:

OPERACIONES CON FUNCIONES

Suma de funciones

Sean f y g dos funciones reales de variable real definidas en un mismo intervalo. Se llama suma de ambas funciones, y se representa por f + g, a la función definida por

Resta de funciones

Del mismo modo que se ha definido la suma de funciones, se define la resta de dos funciones reales de variable real f y g, como la función

Para que esto sea posible es necesario que f y g estén definidas en un mismo intervalo.

Multiplicación de funciones

Sean f y g dos funciones reales de variable real, y definidas en un mismo intervalo. Se llama función producto de f y g a la función definida por

División de funciones

Dadas dos funciones reales de variable real, f y g, y definidas en un mismo intervalo, se llama función cociente de f y g a la función definida por

(La función f/g está definida en todos los puntos en los que la función g no se anula.)

Producto de un número por una función

Dado un número real a y una función f, el producto del número por la función es la función definida por

Ejercicio:

Sean las funciones f(x) = 3x + 1, y g(x) = 2x - 4.

Definir la función f + g y calcular las imágenes de los números 2, -3 y 1/5.

Resolución:

· La función f + g se define como

(f + g) (x) = f(x) + g(x) = x + 1 + 2x - 4 = 5x - 3.

· (f + g) (2) = 5 · 2 - 3 = 7

(f + g) (-3) = 5(-3) - 3 = -18

(f + g) (1/5) = 5 · 1/5 - 3 = -2

Obsérvese que si se calculan las imágenes de f y g por separado y se suman, el resultado es el mismo.

Por ejemplo, para la imagen del 2,

‚ Dadas las funciones f (x) = x² - 3, y g(x) = x + 3, definir la función (f - g)(x).

Calcular las imágenes de 1/3, -2 y 0 mediante la función f - g.

Resolución:

Calculando las imágenes de los números mediante las funciones f y g por separado, y efectuando la resta, se obtiene el mismo resultado.

Resolución:

Calculando las imágenes de los números mediante las funciones f y g por separado, y multiplicando después, se obtienen los mismos resultados.

„ Dadas las funciones f(x) = -x - 1, y g(x) = 2x + 3, definir f/g.

Resolución:

La función f/g está definida para todos los números reales, salvo para x = -3/2, donde la función g se anula.

Calculando por separado las imágenes de los números mediante las funciones f y g, y después efectuando su cociente, se obtienen los mismos resultados.